들어가기에 앞서 본 페이지는 탐구의 목적에 비중이 있기 때문에
간략한 요약을 원한다면 다른 전문가의 블로그를 참조하는 것을 추천한다.
1) 손실함수가 무엇인가
머신러닝에서의 손실함수(loss function)는 모델이 얼마나 높은 정확도로 예측하는지를 평가하는 지표로 쓰인다.
정확하게는, 추론값과 정답값을 기반으로 오차값을 리턴하여 모델의 가중치를 조정할 수 있도록 사용된다.
2) 손실함수의 종류가 나뉘는 이유가 무엇일까
어떤 모델이 추론한 결과가 종합적으로 얼마나 틀렸는지의 정도를 알아낼 수 있을까?
알아낼 방법은 다양할 것이다.
큰 오차가 없어야 하는 데이터라면 작은 오차도 최대화하여 그 정도를 매길 수 있을 것이고,
평균 오차가 적어야 하는 데이터라면 오차의 크기와 무관하게 일정하게 가중하여 그 정도를 매길수 있을 것이다.
이와 같이 추론할 대상에 따라 오차값을 다루는 방식이 다르므로, 손실함수의 종류도 다양해질 수 밖에 없다.
손실함수의 대표적인 예시로 MAE와 MSE가 있다.
- 평균 제곱 오차(MSE) :
- 사용 : 큰 오차를 빠르게 줄이고자 할 때나 이상치가 별로 없는 데이터에 주로 사용한다.
- 특징 : 오차의 정도에 따라 상대적으로 가중된다.
- 평균 절댓값 오차(MAE)
- 사용 : 이상치가 많은 데이터에 사용된다.
- 특징 : 오차의 정도와 상관없이 일정하게 가중된다.
각 모델에 대해 아래에서 자세히 알아보겠다.
3) 평균 제곱 오차(MSE)
데이터의 각 추론값과 정답값의 차이를 제곱한 수의 합을 데이터 갯수로 나누어서 구하게 된다.
식에서 제곱을 이용하기 때문에 차이가 조금만 벌어져도 오차값이 기하급수적으로 커지게 될 것임을 예상할 수 있다.
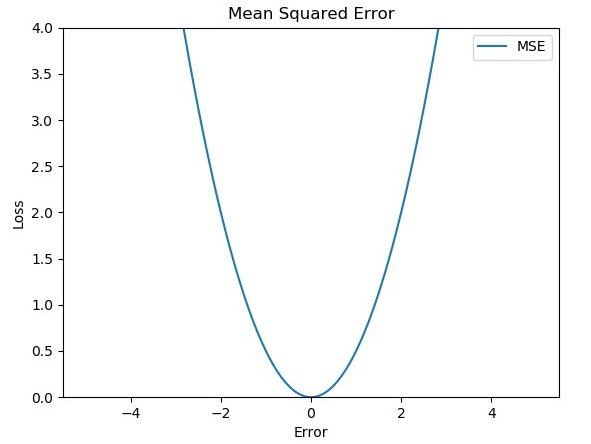
오차값이 크다면, 그만큼 모델의 가중치도 크게 변화하며 오차를 줄이려고 할 것이다.
그러면 큰 오차를 빠르게 줄일 수 있기 때문에 좋을 수 있다.
하지만 다음 예시의 경우 이야기가 다르다. 표를 봐보자.
| 예측값 | 정답값 |
| 5 | 5 |
| 6 | 6 |
| 1 | 1.15 |
| 100 | 274000 |
| 2 | 1.9 |
| 15 | 15 |
위 모델을 보면 전반적으로 추론을 잘 해냈으나
4번째 행의 정답값이 말도 안되게 큰 바람에 모델의 예측이 완전 빗나갔다.
이 경우에 만약 평균 제곱 함수를 사용한다면 오차값은 비정상적으로 커질것이다.
그러면 모델은 이미 충분히 괜찮은 상태였으나 불필요한 가중치 조정이 생기게 된다.
이렇게 되면 시간은 시간대로 더 걸릴거고 전기도 더 쓸거다. 최악의 상황이다.
시험에서 1등급 맞았는데 한 문제를 좀 실수했다고 겁나 줘팬다고 생각해보자.
4) 평균 절댓값 오차(MAE)
앞서 열거한 문제를 해결하기 위해 평균 절댓값 오차가 사용된다.
데이터의 각 추론값과 정답값의 차이를 뺀 수의 절댓값의 합을 데이터 갯수로 나누어서 구하게 된다.
추론값과 정답값의 차이는 결국 1차 함수일거고, 1차 함수는 미분하면 상수이기 때문에 기울기가 아래와 같을 것임을 알 수 있다.
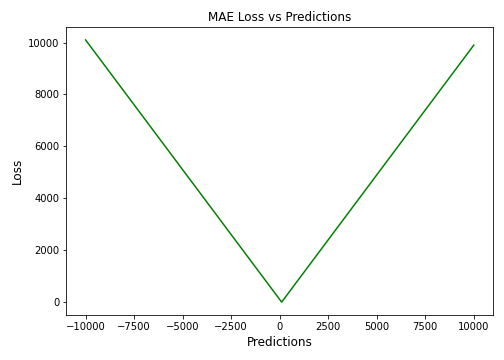
오차의 크기와 무관하게 기울기는 늘 일정하기 때문에, MSE보다 이상치가 영향을 주는 정도가 약할 것이다.
그러면 장점만 있냐하면 그건 아니다. 단점은 아래와 같다.
- 학습 속도가 MSE에 비하여 느리다
- 절댓값을 이용하기 때문에 방향 값을 알수가 없다(정답값에 비해 작은지, 큰지 구분하기 어려움)
- 모든 점에서 연속 가능하지 않기 때문에 작업할 때 추가 처리가 필요하다
5) 정리
간단하게 주요 손실함수의 개념 및 장단점을 이야기해보았다.
모델이 사용될 데이터의 상태와 추론할 목표에 따라서 손실함수를 선택하여야 모델의 효율적 학습에 도움이 되겠다.